いきなりDSPを立ち上げても、実際にはどういった処理をするのかを知る必要があると思いますので、まず移動平均(一種のローパス・フィルタ)を通してディジタル信号処理の例を見てもらいます。
『FIRディジタル・フィルタ』を一言で言うと『移動平均』の拡張であるといえます。
4つの値で移動平均を行った場合を説明します。その様子を下の図1に示します。
図1では今の時間を含めから3つ手前までの値を足し合わせ4で割ります。(同図上)つまり、4つの値の平均をとります。これを、新しく1つサンプルするごとに行います。(同図下)この移動平均の適用例を図2に示します。
図2の元のデータでは細かくでこぼこしている(高い周波数成分がある)のに対し、移動平均を行った後では大きな波(低い周波数成分)だけが現れています。この移動平均は低い周波数成分だけを通す、すなわちローパス・フィルタの役割をしているわけです。
この処理のブロック図を書くと図3のようになります。
現在の値をx[n]とし、1つ前にサンプルしたものをx[n-1]、同様にx[n-2]、x[n-3]と表します。z-1は入力を1サンプル時間遅らせて出力する記号です。現在の値と1サンプルずつ遅らせたものを3つ足し合わせ、その値を1/4にし平均をとっています。
この移動平均を実行するためのプログラムを書くと次のようになります。
(模式的に書きます。)
|
xに現在サンプルした値が入っており、yにその結果が入る。
x1は現在から1サンプル前の値、x2は現在から2サンプル前の値、同様にx3
y = x;
y = y + x1;
y = y + x2;
y = y + x3; /* 4つの値を足し合わせる */
y = y / 4; /* 4つの平均をとる */
x3 = x2; /* x3に1つ前の値であるx2を代入する */
x2 = x1;
x1 = x;
この処理を1サンプル取り込むごとに実行する。
|
|
このプログラムを実装することによりローパス・フィルタが実現できます。ちなみに、このフィルタの周波数特性を図4に示します。
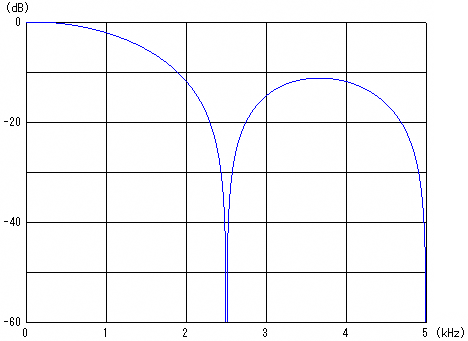
図4 移動平均の周波数特性(サンプリング周波数:10kHz)
この例では、4つの値の平均をただとっただけですが、実際は『ある定数』との乗算を行ってから足しあわせます。(図5)このフィルタを『FIRディジタル・フィルタと』いいます。
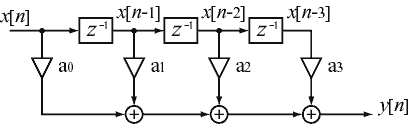
図5 FIRディジタル・フィルタ
このa0,a1,a2,…の定数や、遅延器の数を変えることによりさまざまなフィルタを
実現できます。(ローパス、ハイパス、バンドパスなど)
多分、みなさまが思っていたより簡単と感じたのではないのでしょうか。ディジタル信号処理自体は簡単な処理の繰り返しによって行われます。
仕様に応じて、構成や定数を決めなければなりませんが、ディジタル信号処理の本に様々なタイプの数式が載っていますので、各自必要に応じたものを利用すれば問題ありません!(アルゴリズム化して実装しなければなりませんが。)
ここではDSPの使い方にフォーカスを置いていますので、ディジタル信号処理としての理論的な点は本を参照してください。
|

